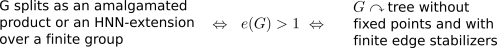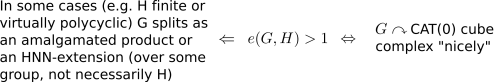The following is largely based on the paper The Tits Alternative for CAT(0) Cubical Complexes by Sageev and Wise.
1.1. The Tits alternative
A group  satisfies the Tits alternative if for all subgroups
satisfies the Tits alternative if for all subgroups  , either
, either  is virtually solvable or it contains a non-abelian free group. One way to think of this is that a group satisfying the Tits alternative has either “small” subgroups (subgroups and quotients of solvable groups are solvable), or “large” subgroups (extensions by groups containing a free group contain a free group). The term originates from the work of Jacques Tits in which he showed that finitely generated linear groups have this property (later named the Tits alternative).
is virtually solvable or it contains a non-abelian free group. One way to think of this is that a group satisfying the Tits alternative has either “small” subgroups (subgroups and quotients of solvable groups are solvable), or “large” subgroups (extensions by groups containing a free group contain a free group). The term originates from the work of Jacques Tits in which he showed that finitely generated linear groups have this property (later named the Tits alternative).
1.2. Known results
The following groups are known to satisfy the Tits alternative:
- Finitely generated linear groups (Tits)
- hyperbolic groups (Gromov, Ghys and de la Harpe)
-
 (Bestvina-Feighn-Handel)
(Bestvina-Feighn-Handel)
- mapping class groups of compact surfaces (Ivanov, McCarthy)
- some large subclasses of CAT(0) groups (Ballmann-Swiatkowski, Sageev-Wise, Xie)
Thompson’s group F is an example of a group not satisfying the Tits alternative as it contains no free subgroup of rank greater than one and isn’t virtually solvable (Bleak, for instance, constructs non-virtually solvable subgroups). Another is the Grigorchuk group. In fact any group of intermediate growth can’t satisfy the Tits alternative: it can’t have a non-abelian free subgroup (otherwise its growth would in fact be exponential), and by the Milnor–Wolf theorem, if it were virtually solvable, it would have to have a finite index nilpotent subgroup (implying polynomial growth by Gromov’s theorem) or an exponentially growing solvable subgroup (again contradicting intermediate growth).
It’s still an open question whether the Tits alternative holds for all  groups, i.e. for groups which act properly and cocompactly by isometries on some
groups, i.e. for groups which act properly and cocompactly by isometries on some  space.
space.
1.3. Hyperbolic groups
In case of hyperbolic groups, a stronger version of the Tits alternative holds:
Theorem 1. A subgroup of a hyperbolic group either
- is finite,
- is virtually infinite cyclic, or
- contains a nonabelian free group.
An elementary proof of the above in the case where the subgroup is torsion free is presented on Henry Wilton’s geometric group theory blog (a precursor and inspiration for the blog you’re now reading). The general case requires additional results about hyperbolic elements and is presented (in French) in Sur les groupes hyperboliques d’après Mikhael Gromov (Theorem 37, page 157).
1.4. Groups acting on  cube complexes
cube complexes
Theorem 2 (Sageev-Wise). Suppose  acts properly on a finite dimensional
acts properly on a finite dimensional  cube complex
cube complex  and has a bound on the order of finite subgroups. Then any subgroup of
and has a bound on the order of finite subgroups. Then any subgroup of  either contains
either contains 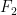 or is virtually abelian.
or is virtually abelian.
In particular, if the group acts on such an  freely (and thus has no non-trivial finite subgroups), its subgroups contain
freely (and thus has no non-trivial finite subgroups), its subgroups contain 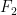 or are virtually abelian.
or are virtually abelian.
I’ll sketch the proof of this theorem following the exposition in the original paper and add a few explanatory details.
We first prove the theorem assuming that  is finitely generated.
is finitely generated.
Since  is assumed to be finite dimensional, we proceed, as you may have already guessed, by induction on the dimension. If the dimension is 0, then the group
is assumed to be finite dimensional, we proceed, as you may have already guessed, by induction on the dimension. If the dimension is 0, then the group  must be finite (since the action is proper), so we’re done. Now we assume the theorem holds for
must be finite (since the action is proper), so we’re done. Now we assume the theorem holds for  acting on all such cube complexes of dimension less than
acting on all such cube complexes of dimension less than  . Assume
. Assume 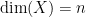 . To apply the induction step, we will identify a proper action of a subgroup of
. To apply the induction step, we will identify a proper action of a subgroup of  on a lower dimensional subcomplex of
on a lower dimensional subcomplex of  . This subcomplex will be a “hyperplane” (defined next) and the subgroup acting will be its stabilizer.
. This subcomplex will be a “hyperplane” (defined next) and the subgroup acting will be its stabilizer.
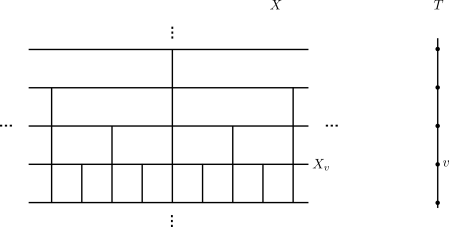
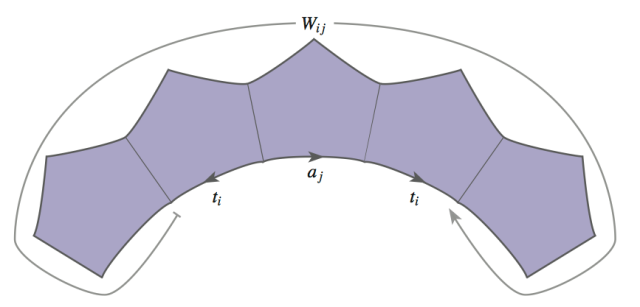
A  cube complex
cube complex  is a cubical cell complex which is simply connected and in which every link is flag. Two edges of
is a cubical cell complex which is simply connected and in which every link is flag. Two edges of  are square equivalent if they are opposite edges of a square of
are square equivalent if they are opposite edges of a square of  . Let
. Let  be an
be an  -cube (identified with the standard unit cube in
-cube (identified with the standard unit cube in 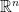 ). A midcube of
). A midcube of  is an intersection of
is an intersection of  with an
with an 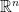 hyperplane parallel to a face of
hyperplane parallel to a face of  and containing its center. For instance, there is only one midcube in an edge, two midcubes in a square, etc.
and containing its center. For instance, there is only one midcube in an edge, two midcubes in a square, etc.

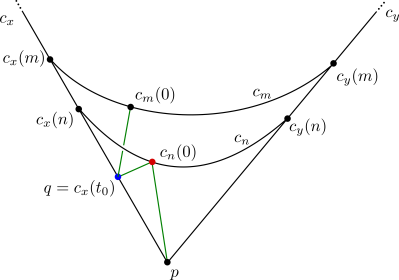
A hyperplane in  is the union of all midcubes meeting the equivalence class of an edge (under the equivalence relation generated by square equivalence). A few facts about hyperplanes:
is the union of all midcubes meeting the equivalence class of an edge (under the equivalence relation generated by square equivalence). A few facts about hyperplanes:
- A hyperplane meets each cube in at most one midcube.
- A hyperplane separates
 into two components.
into two components.
- The
 cube structure on
cube structure on  induces a
induces a  cube structure on any hyperplane in
cube structure on any hyperplane in  .
.
1.5. Tangent: ends of groups
Let  be any finitely generated group, with
be any finitely generated group, with  being the set of generators. Then the number of ends of
being the set of generators. Then the number of ends of  , denoted
, denoted 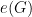 , is the number of components of the boundary
, is the number of components of the boundary 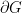 . It’s a classic fact that the number of ends can only equal 0 (when
. It’s a classic fact that the number of ends can only equal 0 (when  is finite), 1 (e.g.
is finite), 1 (e.g. 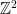 ), 2 (e.g.
), 2 (e.g. 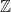 ), or infinity (e.g.
), or infinity (e.g. 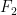 ).
).
The number of ends of a finitely generated group  relative to a subgroup
relative to a subgroup  , denoted
, denoted 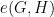 , is the number of ends of the graph
, is the number of ends of the graph 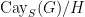 , i.e. the quotient of the Cayley graph of
, i.e. the quotient of the Cayley graph of  by the action of
by the action of  . Equivalently, it is the number of ends of the graph in which vertices are cosets of
. Equivalently, it is the number of ends of the graph in which vertices are cosets of  and vertices
and vertices 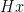 and
and  are connected if and only if
are connected if and only if  .
.
It is a famous result of Stallings that  if and only if
if and only if  splits as an amalgamated product or an HNN-extension over a finite group. In the language of Bass-Serre theory, we have:
splits as an amalgamated product or an HNN-extension over a finite group. In the language of Bass-Serre theory, we have:
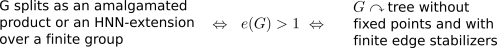
For relative ends, the picture is more complicated:
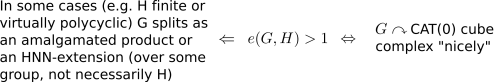
The one of the key theorems which embody the ( ) implication above is the Algebraic Torus Theorem (Dunwoody-Swenson), given below. First, however, we must establish the subgroup with respect to which
) implication above is the Algebraic Torus Theorem (Dunwoody-Swenson), given below. First, however, we must establish the subgroup with respect to which  has multiple ends.
has multiple ends.
Theorem 3 (Sageev). Suppose 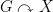 , a finite dimensional
, a finite dimensional  cube complex, without a global fixed point. Then there is a hyperplane
cube complex, without a global fixed point. Then there is a hyperplane 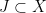 such that
such that 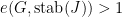 .
.
Theorem 4 (Algebraic Torus). Suppose  is finitely generated, and
is finitely generated, and  , a subgroup of
, a subgroup of  , is virtually polycyclic with
, is virtually polycyclic with 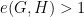 . Then one of the following holds.
. Then one of the following holds.
-
 is virtually polycyclic.
is virtually polycyclic.
- There exists a short exact sequence
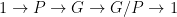
in which 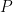 is virtually polycyclic and
is virtually polycyclic and 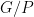 is non-elementary fuchsian (see below).
is non-elementary fuchsian (see below).
-
 splits over a virtually polycyclic group.
splits over a virtually polycyclic group.
1.6. Tangent: fuchsian groups
A fuchsian group is a subgroup of 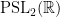 . Thus, a fuchsian group
. Thus, a fuchsian group  acts discretely on the hyperbolic plane
acts discretely on the hyperbolic plane  . Consider the set
. Consider the set  , for some
, for some 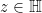 . With respect to the hyperbolic metric on
. With respect to the hyperbolic metric on  , the set
, the set  has no limit points: either in
has no limit points: either in  , since the action is discrete, or in
, since the action is discrete, or in 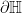 , since every point in
, since every point in  is infinitely far from the boundary. However, considering the Euclidean distance
is infinitely far from the boundary. However, considering the Euclidean distance  inherits by being embedded as the Poincaré disk in
inherits by being embedded as the Poincaré disk in 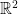 ,
,  may have limit points in
may have limit points in 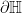 . Basic hyperbolic geometry implies that:
. Basic hyperbolic geometry implies that:
- the limit points occur only in
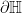 ,
,
- for any other
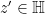 , the sets of limit points of
, the sets of limit points of 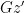 and
and  are identical, and
are identical, and
- the cardinality of the set of limit points is 0, 1, 2 or uncountable.
A fuchsian group is non-elementary when the set of limit points is uncountable. Such a group contains 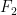 .
.
The non-elementary fuchsian groups are really the only interesting ones: the elementary ones are either finite or virtually cyclic.
Let’s recap the proof so far. We proceed by induction, and assume the theorem true for 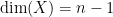 . For
. For  of dimension
of dimension  , since
, since  is infinite and acts properly on
is infinite and acts properly on  , it has no global fixed points. Hence we apply Sageev’s theorem and conclude that there is a hyperplane
, it has no global fixed points. Hence we apply Sageev’s theorem and conclude that there is a hyperplane 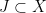 s.t.
s.t. 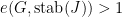 . Let
. Let 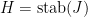 . Then
. Then  acts on
acts on 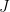 properly. By induction, either
properly. By induction, either  has an
has an 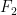 subgroup, and then so does
subgroup, and then so does  so we’re done, or
so we’re done, or  is virtually f.g. abelian. In this case, we apply the Algebraic Torus Theorem to
is virtually f.g. abelian. In this case, we apply the Algebraic Torus Theorem to  and
and  , and conclude that (1)
, and conclude that (1)  is virtually polycyclic, or (2) it has a non-elementary fuchsian quotient, or (3) it splits over a virtually polycyclic group. We deal with these possibilities one by one.
is virtually polycyclic, or (2) it has a non-elementary fuchsian quotient, or (3) it splits over a virtually polycyclic group. We deal with these possibilities one by one.
If  is virtually polycyclic, then we can apply the following two results of Bridson to conclude that it’s in fact virtually abelian.
is virtually polycyclic, then we can apply the following two results of Bridson to conclude that it’s in fact virtually abelian.
Lemma 5.
- If
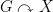 , a
, a  complex with finitely many shapes, then
complex with finitely many shapes, then  acts semi-simply with a discrete set of translation lengths.
acts semi-simply with a discrete set of translation lengths.
- If
 acts semi-simply and properly on a
acts semi-simply and properly on a  space, then any virtually solvable subgroup
space, then any virtually solvable subgroup 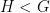 is virtually abelian.
is virtually abelian.
(The number of shapes of a metric cell complex is the number distinct isometry classes of cells. In our case,  has finitely many shapes since every cube of a given dimension is isometric and
has finitely many shapes since every cube of a given dimension is isometric and  is has finite dimension. An action is semi-simple if there are points in the space realizing the translation lengths of each element. I.e., if for every
is has finite dimension. An action is semi-simple if there are points in the space realizing the translation lengths of each element. I.e., if for every 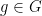 there’s a point realizing
there’s a point realizing 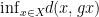 ).
).
If  has a non-elementary fuchsian quotient, which must contain an
has a non-elementary fuchsian quotient, which must contain an 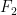 , then
, then  itself must contain an
itself must contain an 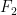 .
.
Finally, suppose  splits over a virtually polycyclic group
splits over a virtually polycyclic group 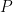 . Then by the first part of Bridson’s lemma above,
. Then by the first part of Bridson’s lemma above,  acts semi-simply, and by the second part,
acts semi-simply, and by the second part, 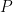 must be virtually abelian. We analyze amalgamated products and HNN-extensions separately.
must be virtually abelian. We analyze amalgamated products and HNN-extensions separately.
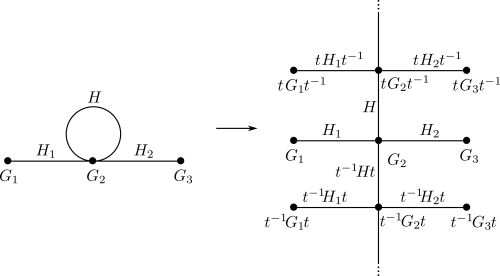
Suppose  . If
. If ![{[A:P] > 2}](https://s0.wp.com/latex.php?latex=%7B%5BA%3AP%5D+%3E+2%7D&bg=ffffff&fg=000000&s=0&c=20201002) or
or ![{[B:P]>2}](https://s0.wp.com/latex.php?latex=%7B%5BB%3AP%5D%3E2%7D&bg=ffffff&fg=000000&s=0&c=20201002) , then
, then  contains an
contains an 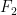 , by the normal form theorem for amalgamated products. If
, by the normal form theorem for amalgamated products. If ![{[A:P] = [B:P] = 2}](https://s0.wp.com/latex.php?latex=%7B%5BA%3AP%5D+%3D+%5BB%3AP%5D+%3D+2%7D&bg=ffffff&fg=000000&s=0&c=20201002) , then the Bass-Serre tree, on which
, then the Bass-Serre tree, on which  acts, is homeomorphic to a line in which every edge is stabilized by a conjugate of
acts, is homeomorphic to a line in which every edge is stabilized by a conjugate of 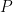 . Thus there’s an index 2 subgroup
. Thus there’s an index 2 subgroup 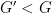 acting by translations and
acting by translations and  . Hence
. Hence  , and so
, and so  is virtually polycyclic and hence virtually abelian by Bridson’s lemma. This takes care of the amalgamated product case. To analyze an HNN-extension by
is virtually polycyclic and hence virtually abelian by Bridson’s lemma. This takes care of the amalgamated product case. To analyze an HNN-extension by 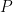 , as well as to prove this theorem for non-finitely generated
, as well as to prove this theorem for non-finitely generated  , another theorem is required.
, another theorem is required.
Theorem 6 (Bridson-Haefliger). Suppose 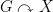 by semi-simple isometries and
by semi-simple isometries and  is
is  . Suppose also that
. Suppose also that
- there’s a bound on the dimension of isometrically embedded flats,
- the set of translation lengths of
 is discrete at 0, and
is discrete at 0, and
- there is a bound on the order of finite subgroups.
Then any ascending sequence of virtually abelian subgroups stabilizes.
Suppose  , with
, with 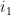 and
and 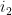 being the two injections of
being the two injections of 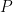 into
into 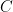 . If
. If ![{[C:i_1(P)] > 1}](https://s0.wp.com/latex.php?latex=%7B%5BC%3Ai_1%28P%29%5D+%3E+1%7D&bg=ffffff&fg=000000&s=0&c=20201002) and
and ![{[C:i_2(P)] > 1}](https://s0.wp.com/latex.php?latex=%7B%5BC%3Ai_2%28P%29%5D+%3E+1%7D&bg=ffffff&fg=000000&s=0&c=20201002) , then by the normal form theorem for HNN-extensions,
, then by the normal form theorem for HNN-extensions,  has an
has an 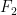 subgroup. If
subgroup. If ![{[C:i_1(P)] = 1}](https://s0.wp.com/latex.php?latex=%7B%5BC%3Ai_1%28P%29%5D+%3D+1%7D&bg=ffffff&fg=000000&s=0&c=20201002) , then
, then ![{[C:i_2(P)] = 1}](https://s0.wp.com/latex.php?latex=%7B%5BC%3Ai_2%28P%29%5D+%3D+1%7D&bg=ffffff&fg=000000&s=0&c=20201002) . [Otherwise, if
. [Otherwise, if 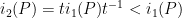 , consider the following subgroups of
, consider the following subgroups of  :
:
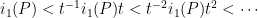
By the Bridson-Haefliger theorem above, this sequence must stabilize, hence  .] Then
.] Then 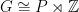 , and by Bridson’s lemma,
, and by Bridson’s lemma,  is virtually abelian.
is virtually abelian.
This finishes the proof for finitely generated  . If
. If  is not finitely generated, it contains an ascending, non-stabilizing sequence of finitely generated subgroups
is not finitely generated, it contains an ascending, non-stabilizing sequence of finitely generated subgroups
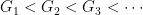
If any 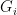 contains an
contains an 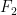 , we’re done. If not, then by the theorem applied to finitely generated groups, each is virtually abelian. Then conditions of the Bridson-Haefliger theorem above are satisfied, however, so a non-stabilizing ascending sequence is impossible. Hence if
, we’re done. If not, then by the theorem applied to finitely generated groups, each is virtually abelian. Then conditions of the Bridson-Haefliger theorem above are satisfied, however, so a non-stabilizing ascending sequence is impossible. Hence if  is not finitely generated, it contains an
is not finitely generated, it contains an 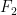 .
.