Non-positively curved groups IV – quadratic isoperimetric functions

The main sources for this post are the slides for Riley’s talk “How wild can a group with quadratic Dehn function be?” and Section 4.1 of Sapir’s article “Asymptotic invariants, complexity of groups and related problems”.

In Euclidean space, a loop of length ${L}$ can be spanned by a disc of area at most a constant times ${L^2}$ . (Picture a film spanning a wire loop that has been lifted out of soap solution.) This is the classical fact that Euclidean space enjoys a quadratic isoperimetric function. This post concerns the groups that share this geometric feature.

Our context is finitely presented groups, and there, what we mean by enjoying a quadratic isoperimetric function is that the Dehn function is at most a constant times ${n^2}$ . We suggest that subdividing a disc as in this post remains the right way to think about Dehn functions for our purposes, but, for the sake of precision, here’s an equivalent definition. Proving the equivalence (essentially van Kampen’s Lemma — see e.g. this survey) takes some work.

Definition. For a finite presentation ${\langle A \mid R \rangle}$ of a group ${\Gamma}$ , define the Dehn function ${f : \mathbb{N} \rightarrow \mathbb{N}}$ as follows: ${f(n)}$ is the minimal number ${K}$ such that if ${w}$ is a word on ${A^{\pm 1}}$ that represents the identity and has length at most ${n}$ , then ${w}$ equals ${\prod_{i=1}^{K'} {u_i}^{-1} r_i u_i}$ in the free group ${F(A)}$ for some ${K' \leq K}$ , some words ${u_i}$ on ${A^{\pm 1}}$ , and some ${r_i \in R^{\pm 1}}$ .

Combable groups

Admitting a combing ${\{ \sigma_{\gamma} \mid \gamma \in \Gamma \}}$ leads to an upper bound on the Dehn function in terms of the lengths of the combing lines. Define ${L(n)}$ to be the maximum length of ${\sigma_{\gamma}}$ amongst all ${\gamma \in \Gamma}$ a distance at most ${n}$ from the identity.

Theorem. If a finitely generated group admits a combing ${\{ \sigma_{\gamma} \mid \gamma \in \Gamma \}}$ , then it is finitely presentable and its Dehn function is at most a constant times ${n L(n)}$ .

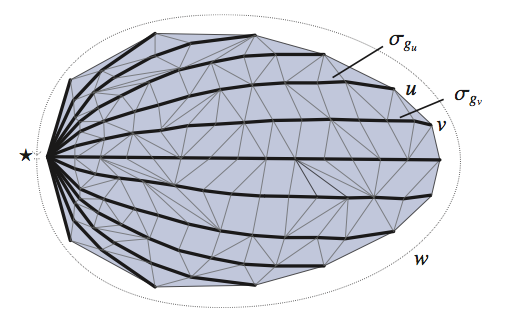
The proof comes down to the “cockelshell” picture below. A word ${w}$ of length ${n}$ representing the identity corresponds to an edge-loop in the Cayley graph based at the identity. Each vertex on on this loop corresponds to a group element ${\gamma}$ — join the vertex to the identity by the combing line ${\sigma_{\gamma}}$ , which has length ${\leq L(n)}$ . Use the ${k}$ –fellow–travelling condition to subdivide the regions between adjacent combing lines into subregions of perimeter at most ${2k+2}$ .

In fact, this approach works whether the combing is synchronous or asynchronous. (In the picture we envisage an asynchronous combing.)

In the event that the combing lines are quasi-geodesics, ${L(n) \preceq n}$ , and so the upper bound is quadratic.

Corollary. Semi-hyperbolic groups (such as automatic or CAT(0) groups) admit quadratic isoperimetric functions.

Examples of groups enjoying a quadratic isoperimetric function

In the light of the results above, it is tempting to hope that groups with quadratic isoperimetric functions be considered non–positively curved. But, in reality, the class is wide. In his 1996 Banff Notes, Gersten wrote of the groups enjoying quadratic isoperimetric functions:

“I call this a zoo, because I am unable to see any pattern in this bestiary of groups. It would be striking if there existed a reasonable characterization of groups with quadratic Dehn functions, which was more enlightening that saying that they have quadratic Dehn functions.”

This comment was prescient given that most of the following examples of groups enjoying a quadratic isoperimetric function (a list from Sapir’s survey) had not been established at the time he was writing:

examples of nilpotent groups of all classes (Allcock, Olshanskii–Sapir, Young),
polycyclic groups that are non-nilpotent (Drutu, Gromov: Filling Riemannian manifolds, J. Diff. Geom. 18 (1983), 1–147),
non-polycyclic metabelian groups with Baumslag-Solitar $\langle a,b \mid b^{-1} a b = a^2 \rangle$ subgroups (Cornulier–Tessera),
all free-by-cyclic groups ${F_n \rtimes {\mathbb Z}}$ (Bridson–Groves),
Stallings’ group (Dison–Elder–Riley–Young),
${\textup{SL}_n({\mathbb Z})}$ for all ${n \geq 5}$ (Young),
Thompson’s group F (Guba).

The proofs of the quadratic isoperimetric functions are varied and, in the most part, hard.

The variety of groups here is wider than what might reasonably be called non–positively curved. For instance Stallings’ group is not of type ${\mathcal{F}_3}$ — that is, it does not have an Eilenberg–MacLane space with finite 3–skeleton, or, to put it more informally, there is no uniform bound on the sizes of the 3-sphere holes in the Cayley graph. This sort of phenomenon does not occur in a non–positively curved setting.

Future directions

Given the wide variety of inmates at the quadratic isoperimetric function zoo, the question is, are they at all special? From the point-of-view of Dehn functions they are the next class of groups after hyperbolic groups, but what more can one say?

Here are a couple of results:

They have simply connected asymptotic cones (Papasoglu).
They have linear filling length functions (Riley).

Papasoglu’s result appears to fail as soon as the Dehn function is at all relaxed. Olshanskii and Sapir have examples with ${n^3}$ Dehn function but non-simply connected cones, and they suggest that ${S}$ -machine technology can be used to improve their examples to ${n^2 \log n}$ .

Filling length is another filling invariant associated to the Word Problem. At the risk of sounding cryptic, all we’ll say here is that it is SPACE in the same sense that the Dehn function is TIME. The proof of the linear upper bound is an elaboration of an argument in Papasoglu’s paper.

It seems that the outstanding question that remains open about groups with quadratic isoperimetric functions is:

Open Question (Rips). Do groups that enjoy a quadratic isoperimetric function have decidable conjugacy problem?

If you relax the isoperimetric function just a small amount to ${n^2 \log n}$ then there are examples due to Olshanskii and Sapir for which there is no algorithm to decide the function conjugacy problem.

Another natural question is —

Open Question. Is the isomorphism problem decidable among the groups that enjoy a quadratic isoperimetric function?

Indeed, one can ask the same thing for the various classes of non-positively curved groups we have discussed in these posts. For instance —

Open Question. Is the isomorphism problem decidable among CAT(0) groups?

Open Question. Is the isomorphism problem decidable among (bi-)automatic groups?

These two questions seem well out of reach at present (especially if they are to be answered positively). But there are two contrasting results we can mention. At one extreme, as we have already discussed, the isomorphism problem for hyperbolic groups has been solved positively. At another extreme, for combable groups, which is a far wider class, the isomorphism problem is undecidable (Bridson) .

Non-positively curved groups IV – quadratic isoperimetric functions

About berstein

Leave a comment Cancel reply

Blogroll

Archives

Meta

Non-positively curved groups IV – quadratic isoperimetric functions

Share this:

Related

About berstein

Leave a comment Cancel reply

Blogroll

Archives

Meta