Quasi-convex subgroups of hyperbolic groups

Our main source for this post is Bridson and Haefliger’s book [BrH].

However, the material has origins in

Alonso, T. Brady, Cooper, Ferlini, Lustig, Mihalik, Shapiro and Short (also ed.),
Gersten and Short,
Ghys and de al Harpe, Sur les groupes hyperboliques d’après Mikhael Gromov, Progr. Math., 83, Birkhauser, 1990, (partial English translation here),
Gromov, Hyperbolic groups, Essays on group theory, MSRI series vol. 8, Springer–Verlag, 1987,
Short, Regular subgroups of automatic groups, MSRI preprint no. 07723–89, 1989.

We’ve completed our overview of the landscape of non–positively curved groups and now turn to the primary subject of this blog — the subgroups. We’ve promised “Here there be dragons!” — but first we’ll cast an eye over the tamer inhabitants. In this post and the next we’ll describe contexts where the subgroup structure can be said to be well–behaved.

We begin here with hyperbolic groups, where the crucial notion in the study of “well–behaved” subgroups was identified by Gromov (Hyperbolic groups, Essays on group theory, MSRI series vol. 8, Springer–Verlag, 1987) as being quasi-convexity.

Quasi–convexity

Here is how the the usual definition of convexity is “quasifyied”.
Definition. A subspace ${Y}$ of a geodesic metric space ${X}$ is quasi–convex when there exists some ${k > 0}$ such that every geodesic in ${X}$ that connects a pair of points in ${Y}$ lies inside the ${k}$ –neighbourhood of ${Y}$ .

Definition. Suppose ${\Gamma}$ is a group with finite generating set $A$ . A subgroup ${H}$ of a group ${\Gamma}$ is quasi–convex if it’s quasi-convex in the Cayley graph ${C_A(\Gamma)}$ .

For hyperbolic groups, this does not depend on ${A}$ .

Lemma 1. Suppose ${\Gamma}$ is a group with finite generating set ${A}$ and that ${H}$ is a ${k}$ –quasi-convex subgroup of ${\Gamma}$ . Then ${H}$ is finitely generated and the inclusion ${H \hookrightarrow \Gamma}$ is a quasi–isometric embedding.

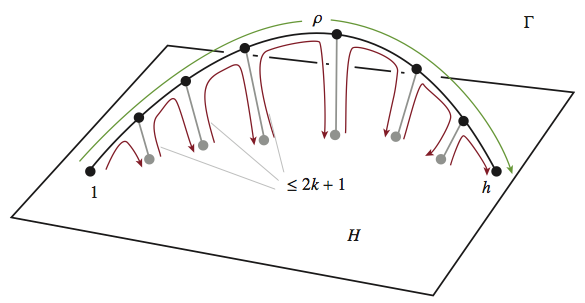
Proof: Let ${B}$ be set of all elements of ${H}$ a distance at most ${2k+1}$ from ${1}$ in ${C_A(\Gamma)}$ . We claim that ${\langle B \rangle =H}$ .

Suppose ${\rho}$ is a geodesic edge–path in ${C_A(\Gamma)}$ from ${1}$ to an element ${h}$ of ${H}$ . Consider inserting detours into the path ${\rho}$ : on arriving at each successive vertex travel to a nearest element of ${H}$ and then back. By the quasi–convexity of ${H}$ , each detour has length at most ${k}$ . So our new path is a concatenation of at most ${d_A(1,h)}$ paths each of which travels between elements of ${H}$ and has length at most ${2k+1}$ — see below.

That ${H \hookrightarrow \Gamma}$ is a quasi–isometric embedding follows from

$\displaystyle \frac{1}{2k+1} d_A(1,h) \ \leq \ d_B(1,h) \ \leq \ d_A(1,h).$

$\Box$

Distortion and chacterizing quasi–convexity in hyperbolic groups

Definition. The distortion ${\textup{Dist}^{\Gamma}_H : {\mathbb N} \rightarrow {\mathbb N}}$ of a finitely generated subgroup ${H}$ in a finitely generated group ${\Gamma}$ , is defined by

$\displaystyle \textup{Dist}^{\Gamma}_H(n) \ = \ \max \{ \, d_H(1,h) \, \mid \, h \in H, \ d_{\Gamma}(1,h) \leq n \, \}.$

Here ${d_{\Gamma}}$ and ${d_H}$ denote word metrics associated to some choices of finite generating sets. Those choices are not important: different choices lead to ${\simeq}$ –equivalent distortion functions.

Definition. ${H}$ is undistorted in ${\Gamma}$ when there exists ${C>0}$ such that ${\textup{Dist}^{\Gamma}_H (n) \leq Cn}$ for all ${n}$ .

Lemma 2. For a finitely generated subgroup ${H}$ of a hyperbolic group ${\Gamma}$ , the following are equivalent.

${H}$ is quasi–convex,
the inclusion ${H \hookrightarrow \Gamma}$ is a quasi-isometric embedding,
${H}$ is undistorted in ${\Gamma}$ .

Proof: Lemma 1 gives 1 ${\implies}$ 2. For 2 ${\implies}$ 1, note that a geodesic in the Cayley graph of ${H}$ (with respect to some finite generating set) connecting a pair of elements ${h_1, h_2 \in H}$ maps to a quasi-geodesic connecting them in the Cayley graph of ${\Gamma}$ (with respect to some finite generating set) since ${H \hookrightarrow \Gamma}$ is a quasi-isometric embedding. But, as ${\Gamma}$ is ${\delta}$ –hyperbolic, that quasi–geodesic is close to any geodesic connecting ${h_1}$ to ${h_2}$ (as we’ve previously discussed), and so any geodesic in the Cayley graph of ${\Gamma}$ between ${h_1}$ and ${h_2}$ is in some uniform neighbourhood of ${H}$ . For 2 ${\Leftrightarrow}$ 3, unravel the definitions to see they are two ways of expressing the same condition. $\Box$

Quasi–convex subgroups are hyperbolic

Theorem 1. Quasi–convex subgroups of hyperbolic groups are hyperbolic.

Proof: The work for this was done in Lemma 2. Suppose ${H}$ is a quasi–convex subgroup of a hyperbolic group ${\Gamma}$ . A geodesic triangle ${\Delta}$ in (a Cayley graph of) ${H}$ becomes a quasi–geodesic triangle in (a Cayley graph of) ${\Gamma}$ , since ${H \hookrightarrow \Gamma}$ is a quasi-isometric embedding. But in ${\delta}$ –hyperbolic spaces, quasi–geodesic are uniformly close to geodesics and geodesic triangles are ${\delta}$ –thin, so ${\Delta}$ is uniformly thin in ${\Gamma}$ and hence also in ${H}$ . $\Box$

The converse to Theorem 1 is false. As we’ll see in some future post (e.g. on Cannon–Thurston maps or on hydra groups), there are hyperbolic (finite rank free, indeed) subgroups of hyperbolic groups that are heavily distorted.

Applications of quasi–convexity
The applications we will draw are that ${{\mathbb Z}^2}$ is never a subgroup of a hyperbolic group and that ${{\mathbb Z}}$ subgroups are always undistorted.

First we need:

Lemma 3 (adapted from [BrH], pages 476–477). If ${H_1}$ and ${H_2}$ are ${k}$ –quasi-convex subgroups of a group ${\Gamma}$ with finite generating set ${A}$ , then their intersection is quasi–convex.

Proof: Let ${d}$ denote the word metric on ${\Gamma}$ with respect to ${A}$ . Let

$\displaystyle K = | \{ \, g \in \Gamma \, \mid \, d(1,g) \leq k \, \} |^2.$

We will show that ${H_1 \cap H_2}$ is ${K}$ –quasi–convex. It is enough to prove that if ${w}$ is a geodesic word on ${A^{\pm 1}}$ representing an element of ${H_1 \cap H_2}$ and ${u}$ is a prefix of ${w}$ , then ${u}$ represents an element of ${\Gamma}$ a distance at most ${K}$ from ${H_1 \cap H_2}$ .

Let ${\Omega}$ be the set of words ${v}$ such that ${uv \in H_1 \cap H_2}$ and for every prefix ${v'}$ of ${v}$ , the group element represented by ${uv'}$ is a distance at most ${k}$ from each of ${H_1}$ and ${H_2}$ . This set is non–empty as one could take ${v}$ to be the suffix of ${w}$ such that ${uv=w}$ as words.

Let ${v}$ be a minimal length word in ${\Omega}$ . We claim that ${\ell(v) \leq K}$ , which will complete the proof of the lemma. Well, suppose ${v^1}$ and ${v^2}$ are prefixes of ${v}$ and ${x_i^j}$ , for ${i,j \in \{1, 2\}}$ , are group elements with ${d(1,x_i^j) \leq k}$ such that ${wv^j x_i^j}$ represent elements of ${H_i}$ . Suppose ${\ell(v_1) < \ell(v_2)}$ — then, as words, ${v_2 = v_1 v_3}$ and ${v = v_1 v_3 v_4}$ for some words ${v_3}$ and ${v_4}$ . If ${(x_1^1, x_2^1) = (x_1^2, x_2^2)}$ , then ${v_1 v_4}$ would be a shorter word than ${v}$ in ${\Omega}$ . So, as there are at most ${K}$ possibilities for the pairs ${(x_1^j, x_2^j)}$ , the length of ${v}$ is at most ${K}$ . $\Box$

Incidentally, our next lemma implies the Conjugacy Problem is decidable in hyperbolic groups. (In fact, it also works in semi–hyperbolic groups.)

Lemma 4. Suppose ${\Gamma}$ is a hyperbolic group and ${d}$ denotes the word metric on ${\Gamma}$ with respect to finite generating set ${A}$ . Then there is a constant ${C}$ such that if ${g}$ and ${h}$ are conjugate elements in ${\Gamma}$ and ${M := \max \{ d(1,g), d(1,h) \}}$ , then there is a word ${v}$ such that ${h = v^{-1}gv}$ in ${\Gamma}$ and ${\ell(v) \ \leq C^{M}}$ .

Proof: Let ${v}$ be a minimal length word such that ${h =v^{-1} g v}$ in ${\Gamma}$ . Let ${v_i}$ denote the length– ${i}$ prefix of ${v}$ , and let ${u_i}$ be a minimal length word such that ${u_i = {v_i}^{-1} g v_i}$ in ${\Gamma}$ . (See below.) The words ${u_i}$ and ${u_j}$ must be different for all ${i < j}$ between ${0}$ and ${\ell(v)}$ , as otherwise we could find a word ${\hat{v}}$ shorter than ${v}$ such that ${h =\hat{v}^{-1} g \hat{v}}$ : if ${v_j = v_i v'}$ and ${v = v_j v''}$ as words, then take ${\hat{v} = v_i v''}$ .

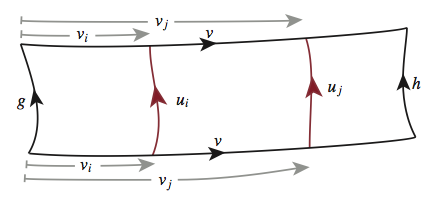
By the convexity of the metric, there is a constant ${k}$ , depending only on ${\Gamma}$ and ${A}$ such that ${\ell(u_i) \leq kM}$ for all ${i}$ . But there are no more than ${(1+2 |A|)^{kM}}$ words of length at most ${kM}$ , which proves the lemma. $\Box$

Proposition 1. (adapted from [BrH], pages 477–478). The centralizer ${C(g)}$ of any element ${g}$ in a hyperbolic group ${\Gamma}$ is quasi-convex.
Proof: Fix a finite generating set ${A}$ for ${\Gamma}$ . Suppose ${\gamma \in C(g)}$ is represented by a geodesic word ${w}$ and ${u}$ is a prefix of ${w}$ . We aim to show that there is a constant ${L}$ , depending only on ${\Gamma}$ , ${A}$ and ${g}$ such that the group element represented by ${u}$ is within distance ${L}$ from ${C(g)}$ .

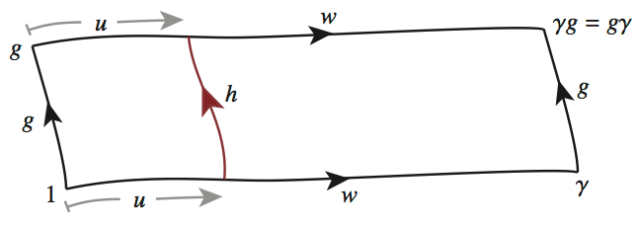
Let ${h = u^{-1} g u}$ . By applying the convexity of the metric to the geodesic rectangle displayed below, we learn there is some constant ${k \geq 1}$ depending only on ${\Gamma}$ and ${A}$ such that ${d(1,h) \leq k d(1,g)}$ .

By definition, ${g}$ and ${h}$ are conjugate. Let ${v}$ be a minimal length word such that ${h =v^{-1} g v}$ . Note that ${uv^{-1} \in C(g)}$ because

$\displaystyle uv^{-1} g \ = \ uhv^{-1} \ = \ guv^{-1}.$

Applying Lemma 4 together with the inequality ${d(1,h) \leq k d(1,g)}$ , we get an upper bound,

$\displaystyle \ell(v) \ \leq \ C^{k d(1,g)},$

which depends only on ${\Gamma}$ , ${A}$ and ${g}$ . Thus $u$ is distance at most $\displaystyle C^{k d(1,g)}$ from $C(g)$ . $\Box$

Another way of stating the conclusion of the next theorem is that the ${{\mathbb Z}}$ subgroups are bi–infinite quasi–geodesics.

Theorem 2 (adapted from [BrH], page 462). ${{\mathbb Z}}$ subgroups of a hyperbolc group are quasi-convex.

Proof: Suppose ${g}$ is an element of infinite order in a hyperbolic group ${\Gamma}$ . By Proposition 1, ${C(g)}$ is quasi–convex, and so, by Theorem 1, is hyperbolic and, in particular, finitely generated. Its centre ${Z(C(g))}$ is the intersection of the centralizers of each of the elements of a finite generating set, so is itself quasi–convex, by Lemma 3. So ${Z(C(g))}$ is hyperbolic by Theorem 1. But ${Z(C(g))}$ is abelian and hyperbolic abelian groups and either finite or virtually ${{\mathbb Z}}$ . As ${Z(C(g))}$ contains ${{\mathbb Z} = \langle g \rangle}$ , it must be virtually ${{\mathbb Z}}$ .

Now the inclusions

$\displaystyle {\mathbb Z} \ = \ \langle g \rangle \ \hookrightarrow \ Z(C(g)) \ \hookrightarrow \ C(g) \ \hookrightarrow \ \Gamma$

are all quasi-isometric embeddings: the first because ${\langle g \rangle}$ is of finite index in ${Z(C(g))}$ , and the second and third by Lemma 2. So the composition ${\langle g \rangle \hookrightarrow \Gamma}$ is a quasi-isometric embedding, and therefore ${\langle g \rangle}$ is quasi–convex by Lemma 2. $\Box$

The theorem above means many non–abelian solvable groups cannot be subgroups of hyperbolic groups — they have distorted ${{\mathbb Z}}$ subgroups on account of calculations such as the following.

Lemma 5. If elements ${g}$ and ${x}$ of a group satisfy the relation ${x^{-1} g^p x = g^q}$ for some integers ${p}$ and ${q}$ , then they satisfy

$\displaystyle x^{-m} g^{p^m} x^m = g^{q^m}$

for all integers ${m \geq 0}$ .
Proof: Induct on ${m}$ :

$\displaystyle \begin{array}{rl} x^{-m-1} g^{p^{m+1}} x^{m+1} & = \ x^{-m} \, x^{-1} (g^p)^{p^m} x \, x^m \\ & = \ x^{-m} \, (x^{-1} g^p x)^{p^m} \, x^m \\ & = \ x^{-m} \, (g^q)^{p^m} \, x^m \\ &= \ ( x^{-m} \, g^{p^m} \, x^m)^q \\ & = \ g^{q^{m+1}}. \end{array}$

$\Box$

The following proposition appears in Gromov’s original article on hyperbolic groups, but his proof is very different: he defines and analyzes the boundary of ${\Gamma}$ .

Proposition 2 (adapted from [BrH], page 462). If ${g}$ is an infinite order element of a hyperbolic group ${\Gamma}$ , then ${\langle g \rangle}$ is a finite index subgroup of its centralizer ${C(g)}$ .

Proof: Fix a finite generating set ${A}$ for ${\Gamma}$ and a ${\delta >0}$ such that ${C_A(\Gamma)}$ is ${\delta}$ –hyperbolic. Lemma 5 implies that the positive powers of ${g}$ are in distinct conjugacy classes since if ${x^{-1} g^p x = g^q}$ for some ${x \in \Gamma}$ and some integers ${p}$ and ${q}$ with ${|p| \neq |q|}$ , then

$\displaystyle d(1, g^{q^m}) \ \leq \ 2m d(1,x) + |p|^m d(1,g)$

and ${\langle g \rangle \hookrightarrow \Gamma}$ would fail to be a quasi–isometric embedding. So, by replacing ${g}$ with a power if necessary, we may assume ${g}$ is not conjugate to an element of ${\Gamma}$ within a distance ${4 \delta +2}$ from ${1}$ .

Now suppose ${h \in C(g)}$ . We aim to show that ${d(h, \langle g \rangle) \leq K}$ where ${ K : = 2 d(1,g) + 4\delta}$ , which will suffice to prove the proposition. We will suppose otherwise and seek a contradiction.

Suppose ${d(h, \langle g \rangle) = d(h, g^r) >K}$ . By replacing ${h}$ by ${g^{-r} h}$ (which is also in ${C(g)}$ ) we can assume ${d(h,1) >K}$ .

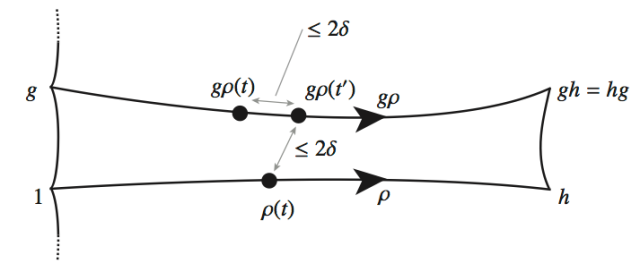
Let ${\rho}$ be a geodesic edge–path in ${C_A(\Gamma)}$ from ${1}$ to ${h}$ , parametrized proportional to arc–length — so ${\rho(t)}$ is a distance ${t}$ from ${1}$ . The translate ${g \rho}$ is a geodesic edge–path from ${g}$ to ${gh=hg}$ . Consider a geodesic rectangle which has ${\rho}$ and ${g\rho}$ as two of its sides:

The fact that geodesic triangles in ${C_A(\Gamma)}$ are ${\delta}$ –thin implies that for all ${t}$ , the point ${\rho(t)}$ is within a distance ${2\delta}$ from one of the other three sides of the rectangle. The assumption that ${d(h,1) >K}$ allows us to choose a ${t}$ for which that other side must be ${g\rho}$ — that is, there is some ${t'}$ such that ${d( \rho(t), g \rho(t') ) \leq 2 \delta}$ . But ${t = d(\langle g \rangle, \rho(t))}$ and ${t' = d(\langle g \rangle, g\rho(t'))}$ , so ${| t- t'| \leq 2 \delta}$ . And therefore, ${d( \rho(t), g \rho(t)) \leq 4\delta}$ .

Let ${x}$ be a group element (i.e. a vertex) on ${\rho}$ closest to ${\rho(t)}$ . Then ${d( x, g x ) \leq 4\delta + 2}$ and so ${d( 1, x^{-1} g x ) \leq 4\delta + 2}$ , which is a contradiction. $\Box$

As an immediate consequence of Proposition 2, we have:

Theorem 3. Abelian subgroups of hyperbolic groups are either finite or virtually ${{\mathbb Z}}$ . In particular, ${{\mathbb Z}^2}$ is never a subgroup of a hyperbolic group.

Quasi-convex subgroups of hyperbolic groups

About berstein

Leave a comment Cancel reply

Blogroll

Archives

Meta

Quasi-convex subgroups of hyperbolic groups

Share this:

Related

About berstein

Leave a comment Cancel reply

Blogroll

Archives

Meta